El Problema de Monty Hall
AVISO: Este artículo no pretende fomentar el juego, ni la ludopaía. Se trata de un análisis enfocado en las matemáticas del juego, donde se explica si el juego puede ser rentable o no y como analizarlo.
Bienvenidos a uno de los problemas mas curiosos de las matemáticas, el problema de Monty Hall.
1.Descripción del problema
2.Análisis intuitivo
3.Simulador de Monty Hall
4.Análisis matemático
4.1.Análisis matemático con probabilidad condicional
5.Solución intuitiva
6.Explicación
7.Conclusiones
1.Descripción del problema
Imaginad que estáis en un concurso y que yo soy el presentador
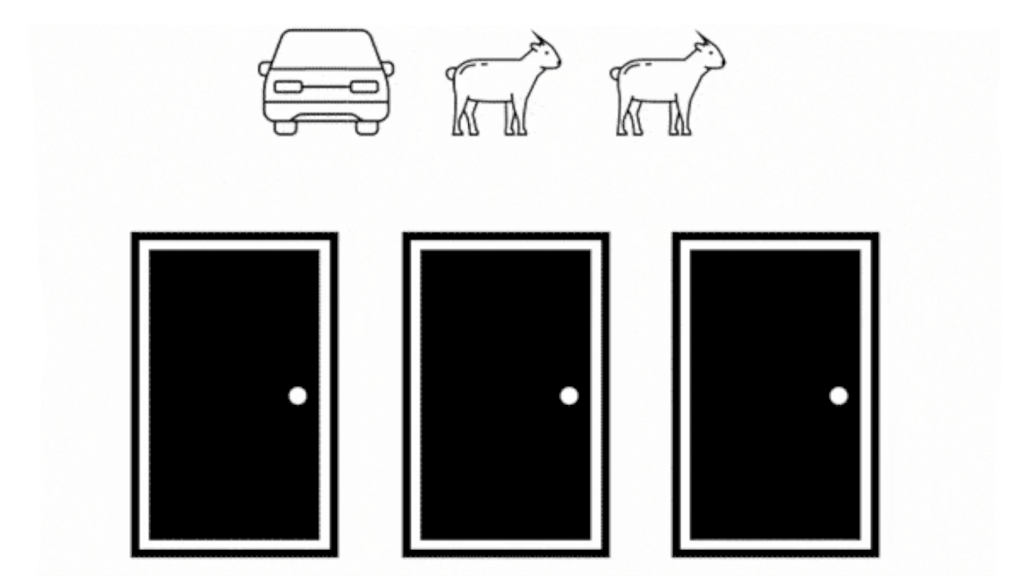
Detrás de una de estas 3 puertas hay un coche nuevo. Y detrás de las otras dos hay cabras (si cabras!!).
Tenéis que elegir una puerta y vamos a suponer que para ejemplo que elegís la puerta 1 (recordad que tenéis que ganar el coche nuevo y no una cabra…)
Yo que puedo ver lo que hay detrás de cada puerta descarto una de las puertas que tiene una cabra, abriendo la número 3 en este caso, y ahora os hago la siguiente pregunta, ¿quieres cambiar la puerta 1 por la 2?, o lo mas importante para el objetivo de este video, ¿crees que eso importa?
El problema de Monty Hall es uno de los problemas más famosos de probabilidad y viene del concurso televisivo de los 70 Let’s Make a Deal. El nombre hace referencia a su famoso presentador, y a su conocido juego de las 3 puertas. Donde se escondía un coche entre una de ellas, y el concursante debía elegir una puerta. Tras descartar otra de las puertas, Monty Hall preguntaba al concursante si quería cambiar de puerta o quedarse la que había elegido. Y es aquí donde empieza el verdadero juego.
2.Análisis intuitivo
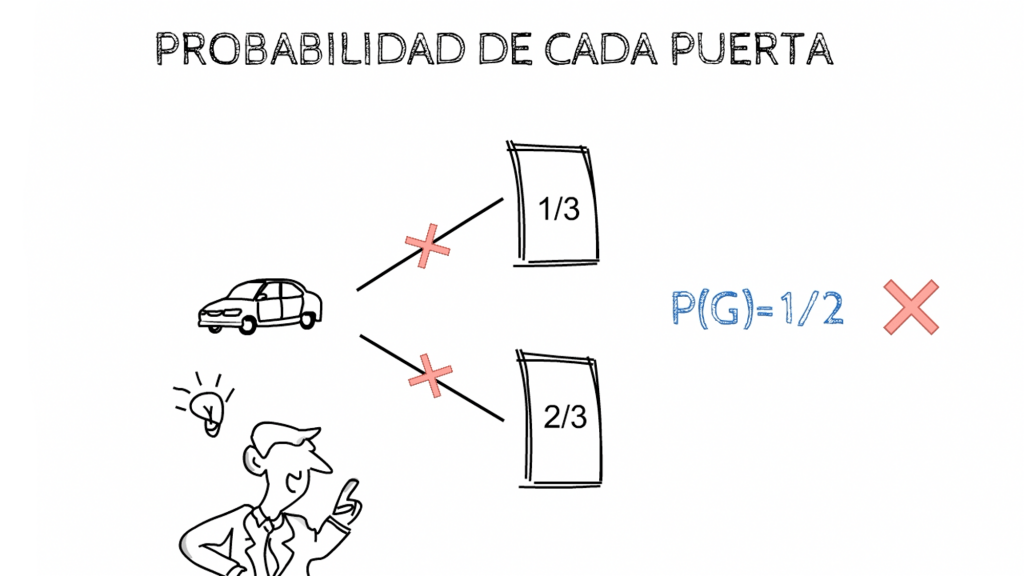
Estoy seguro que muchos de vosotros pensáis que no existe diferencia entre quedaros la puerta o cambiarla. Si quedan dos puertas y un coche, cualquiera de las dos opciones es lo mismo ya que si cambiáis la puerta podéis ganar o perder el coche y si no la cambiáis también podéis ganar o perder, lo cual deja a cada puerta con un 50% de probabilidad. Pero, es eso cierto?
Vuestra intuición puede deciros que si, pero creéis que vuestra intuición ha analizado el problema correctamente, ¿crees que puedes confiar en tu instinto?
3.Simulador Monty Hall
Para salir de dudas he creado un simulador que recrea las reglas de este juego y vamos a ver que resultados nos ofrece para ambas elecciones, así que, no os lo perdáis:
Este hace exactamente lo que hemos descrito, así vamos empezamos a jugar y nos pide elegir una puerta, la elegimos y el presentador nos abre otra puerta donde no está el coche. Después nos hace elegir entre cambiar de puerta o quedárnosla.
Quedándonos siempre la puerta:
Vamos a probar primero quedarnos la puerta que hemos elegido, así que jugamos muchas partidas al simulador, y llegamos a la conclusión de que ganamos el coche aproximadamente un 30% de las veces que hemos jugado (que nos muestra el porcentaje de éxito).
Cambiando siempre la puerta:
Si en cambio elegimos cambiar nuestra puerta por la otra, y repetimos esto muchas veces en el simulador, llegamos a la conclusión de que esta vez ganamos el coche aproximadamente un 60% de las veces. Lo cual hace que ambos resultados sean muy diferentes.
¿No te lo crees? Pruébalo tu mismo
Pensábamos que daría igual, pero hemos visto que cambiar de puerta nos hace ganadores en un porcentaje superior que quedarnos la puerta que teníamos, y parece ser bastante superior. Entonces ¿qué está pasando?
4.Análisis Matemático
Si analizamos el problema a nivel matemático nos daremos cuenta que esto es un problema simple de probabilidad, donde todos los posibles resultados del experimento de elegir una puerta son 3:
elegir coche, elegir una cabra, o elegir la otra cabra.
Los sucesos que necesitamos para resolver el problema son:
G: “Ganar el coche sin cambiar de puerta”
G’: “Ganar el coche cambiando de puerta”
Vamos a estudiar la probabilidad de cada suceso por separado:
Sin cambiar de Puerta
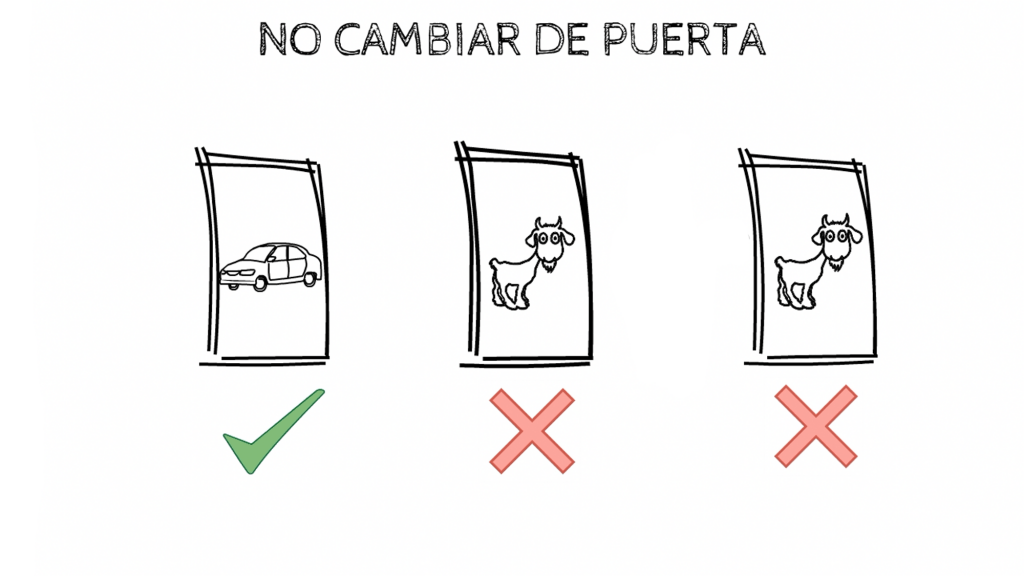
Así que vamos a empezar por no cambiar de puerta.
Si el concursante elige el coche, y no cambia la puerta, ganará el coche seguro, porque aguantará su puerta hasta el final.
De la misma manera si el concursante elige una cabra, y no cambia la puerta, nunca podrá ganar el coche.
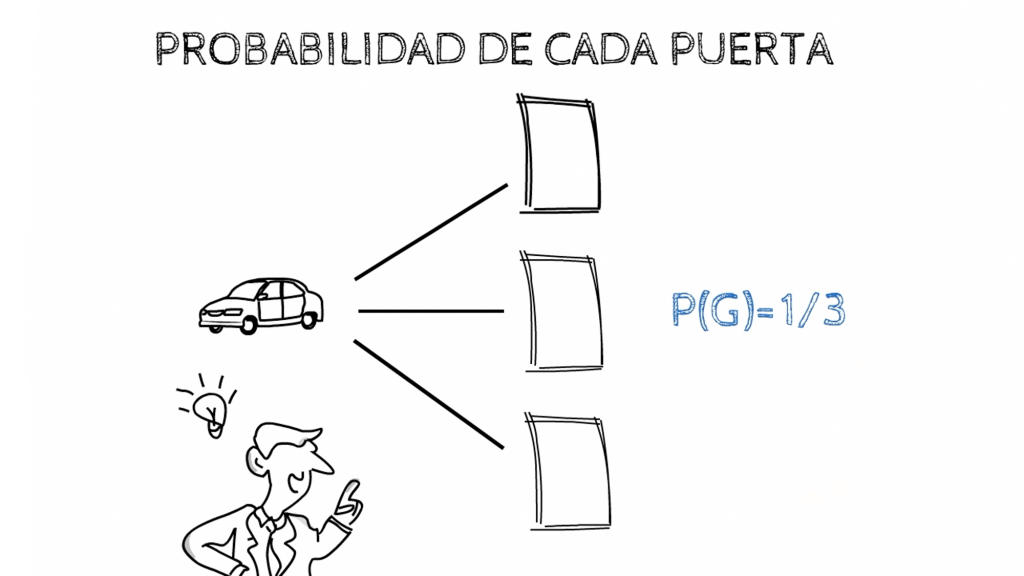
Como hay 1 solo caso donde gana de 3 elecciones posibles, la probabilidad de ganar el coche si no cambia de puerta es de 1/3. Lo cual es aproximadamente un 33,33% de posibilidades de ganar. Eso es 1 de cada 3 veces, lo que os deja en desventaja para poder ganar el coche.
Vamos a ver ahora cual es la probabilidad si decide cambiar de puerta:
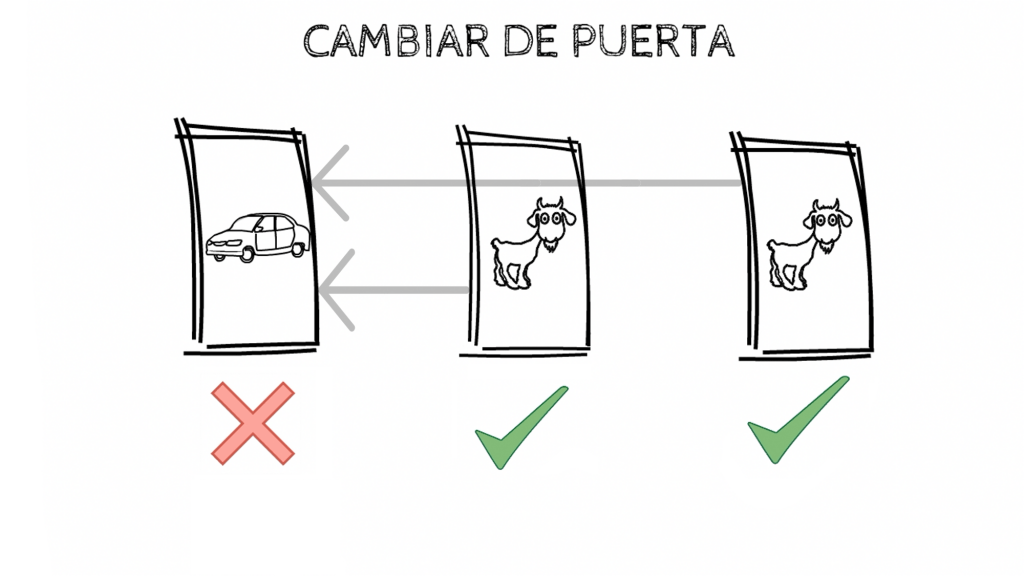
Cambiando de Puerta
Si el concursante elige el coche, y cambia la puerta, ya nunca podrá ganarlo ya que siempre lo cambiará por una cabra. No parece un buen comienzo.
En cambio fijaros que si elige una cabra, el presentador siempre le enseña la otra cabra. Esto descarta automáticamente una de las cabras, lo que implica que el concursante va a cambiar obligatoriamente la cabra que tiene por el coche. Como hay 2 cabras como posibles elecciones ganaremos el coche dos de cada 3 veces por lo que la probabilidad de ganar el coche cambiando de puertas de 2/3. Lo cual duplica las probabilidades de un 33,33 a un 66,66%. Esto nos da una mayor ventaja de ganar el coche.
4.1.Análisis Matemático con Probabilidad Condicional
Los sucesos que necesitamos para resolver el problema son:
A: El concursante elija la puerta donde está el coche”
B: “El concursante elija la puerta donde hay una cabra”
Y por último el suceso que estamos buscando que es:
G: “Que el concursante gane el coche”
La probabilidad de elegir la puerta con el coche como véis es 1 entre 3, y la de elegir la puerta con una cabra es 2/3 , pero, ¿cual es la probabilidad de ganar?
P(A)=1/3
P(B)=2/3
P(G)=?
Para ganar podemos hacerlo de cualquiera de las dos maneras. Elegir el coche y ganar o elegir una cabra y ganar, por tanto
P(G)= P((A y G) ó (B y G))
Lo que traducido al lenguaje matemático sería:
P(G)=P((A∩G) ∪ (B∩G)) (Simplemente tenéis que cambiar los símbolos de y por intersección y la o por unión)
Pues bien la probabilidad de una unión es la suma de probabilidades por lo que podemos separar la probabilidad en 2 más sencillas
P(G)=P(A∩G) + P(B∩G)
Si utilizamos la fórmula de la probabilidad condicionada y despejamos la intersección nos queda:
P(G)=P(G|A)·P(A) + P(G|B)·P(B)
Ahora solo tenemos que calcular la probabilidad de ganar para cada estrategia:
Probabilidad sin cambiar de Puerta
Si hemos decidido quedarnos con la puerta que teníamos:
En el caso de tener un coche, habremos ganado seguro, ya que no lo vamos a cambiar, por lo que la probabilidad condicionada a ese suceso A, será del 100% o 1
P(G|A)=1
Pero esto solo sucederá cuando tengamos un coche y tenemos 1/3 de probabilidades de elegirlo, por lo que la probabilidad de elegir el coche y ganar es de 1·1/3 que es 1/3
P(A)=1/3
P(A∩G)=P(G|A)·P(A)=1·1/3=1/3
En el caso de tener una cabra, si nos quedamos la puerta nunca vamos a ganar por lo que la probabilidad condicionada al suceso será 0, y al multiplicarlo por las probabilidades de tener una cabra sigue siendo 0, lo cual es lógico si ya vemos que es imposible elegir la cabra y ganar el coche desde el principio.
P(G|B)=0
P(B)=2/3
P(B∩G)=P(G|B)·P(B)=0·2/3=0
Si sumamos ambas cantidades tenemos que la probabilidad de ganar si nos quedamos la puerta es de 1/3.
P(G)=P(A∩G) + P(B∩G)=1/3 + 0=1/3
Esto podemos resumirlo como (Coche,Cabra,Cabra)
Probabilidad cambiando de Puerta
Vamos ahora a elegir cambiar de puerta siempre:
En el caso de tener un coche, perdemos el coche seguro, ya que lo vamos a cambiar por una cabra, por lo que la probabilidad condicionada a ese suceso A, será 0
P(G|A)=0
Y la probabilidad de coger el coche y ganar será 0.
P(A)=1/3
P(A∩G)=P(G|A)·P(A)=0·1/3=0
Si en cambio elegimos una cabra, fijaros que el presentador siempre nos elimina la otra cabra, por lo que solo quedará el coche cuando cambiemos de puerta, por lo que ganaremos siempre el coche.
P(G|B)=1
Esto sucederá solamente cuando tengamos una cabra, pero hay que tener en cuenta que la probabilidad de elegir una cabra es 2/3, por lo que la probabilidad de tener una cabra y ganar es de 1·2/3 que es 2/3
P(B)=2/3
P(B∩G)=P(G|B)·P(B)=1·2/3=2/3
Si sumamos ambas cantidades tenemos que la probabilidad de ganar si cambiamos de puerta es de 2/3
P(G)=P(A∩G) + P(B∩G)=0 + 2/3=2/3
Esto podemos resumirlo como (Cabra,Coche,Coche)
5.Solución intuitiva
Si no cambiamos de puerta vemos claro que al haber dos cabras y un coche tenemos 1/3 de posibilidades de ganar el coche.
Si cambiamos de puerta:
- y elegimos el coche siempre perdemos.
- y elegimos una cabra siempre ganamos.
Pero como hay 1 coche y 2 cabras, ganaremos en 2 ocasiones de 3, porque 2 de cada 3 veces elegiremos una cabra.
6.Explicación
Para esto vamos a imaginar de nuevo todos los posibles casos que pueden darse para las 3 puertas. (Fijaros que no diferenciamos el orden de las cabras, ya que eso duplica el numero de casos, pero no cambia la probabilidad)
Cuando elegimos nuestra puerta, tenemos 1/3 de probabilidades de tener el coche. Aunque el presentador abra una puerta, está condicionado por la que nosotros hemos elegido, ya que solo puede abrir una puerta que no sea la nuestra. Eso implica que siempre elimina una cabra de las otras dos puertas, pero nunca de la nuestra.
Fijaros además que en esas 2 puertas siempre hay una cabra para poder eliminar, por lo que el presentador solo descarta una cabra que era segura y nos enseña donde está, pero eso no aumenta las probabilidades de nuestra puerta, ya que nosotros podemos seguir teniendo la otra cabra las mismas veces veces. Esto implica que la puerta que elegimos al principio seguirá teniendo el coche 1 de cada 3 veces y no aumentará sus probabilidades, por mucho que quitemos una puerta.
Sorprendente, que no cambie, pero entonces ¿qué pasa con la otra puerta?
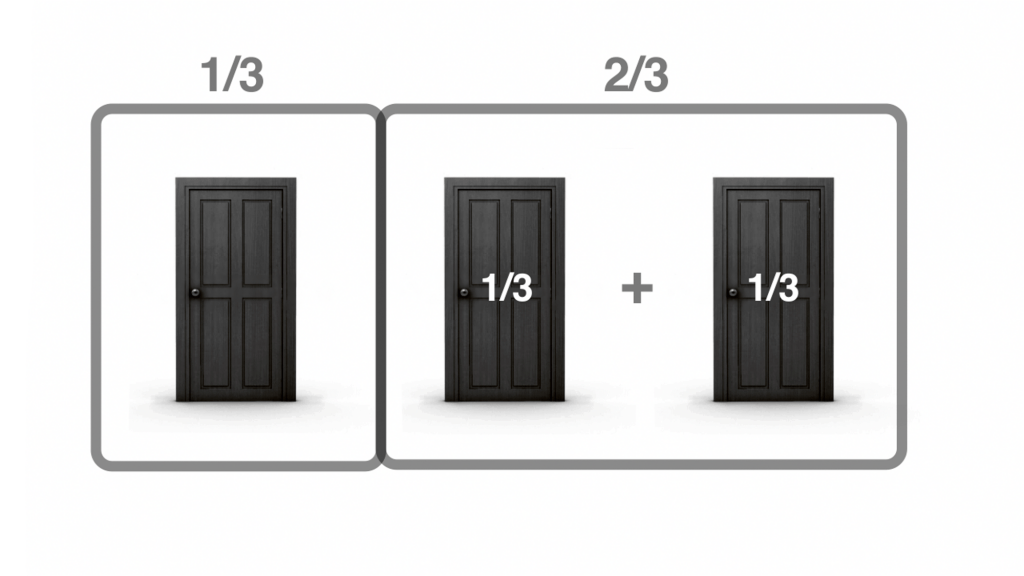
Si nuestra puerta tiene el coche 1 de cada 3 veces, las otras 2 veces estará en las otras dos puertas, por lo que ese grupo de 2 tiene lógicamente mas probabilidades de tener el coche que nuestra puerta. Simplemente tenemos que sumar la probabilidad de cada una.
Cuando el presentador abre una puerta, sabe lo que hay detrás de cada una, por lo que siempre salva el coche en caso de tenerlo. Si las dos puertas tienen el coche 2 de cada 3 veces y siempre descarta una cabra, la puerta que se salve seguirá teniendo el coche 2 de cada 3 veces, por lo que su probabilidad será la misma que tenían ambas puertas pero repartida en una. Por eso debéis cambiarla por esta.
Fijaros también que esta puerta no siempre será la misma y por eso tiene más probabilidad.
Y dicho esto, ¿estás seguro que no quieres cambiar de puerta?
Ampliación de la idea
Imaginaros ahora el mismo juego pero con 20 puertas en lugar de 3. Seguimos eligiendo 1 puerta, y el presentador elimina de la misma manera las puertas que son cabra hasta quedarse con una.
Si olvidamos por un momento nuestra puerta, y pensamos solamente en las 19 que puede eliminar el presentador. Veremos muy claro que 19 puertas tienen mucha más probabilidad que una, por lo que el coche estará la mayoría de veces en una de las puertas que tiene el presentador y solamente una en nuestra puerta. Y si este elimina todas las puertas que son cabra de ese grupo, la puerta que le quede tendrá el coche la mayoría de veces, de la misma manera.
7.Conclusiones
En conclusión el presentador solo elimina cabras de sus puertas, y eso solo puede darle ventaja a alguna sus puertas, pero nunca a la nuestra.
Como hemos visto al final tampoco era tan complicado, pero, ¿por qué no hemos sido capaces de verlo antes?
Al principio el coche puede estar por igual en cualquiera de las puertas, por eso dividimos 1 premio entre 3 puertas, y así calculamos la probabilidad para nuestra puerta. Hasta aquí es correcto.
El problema viene cuando nos abren una puerta.
Cuando el presentador nos da la opción de quedarnos con nuestra puerta o cambiarla, debemos calcular de nuevo la probabilidad de cada puerta para saber cual nos conviene más. Para esto dividimos de la misma manera que antes 1 premio entre 2 puertas, como si el premio pudiera estar por igual en cada una de ellas, pero esto no es así, ya que el descarte que hace el presentador, aumenta solo la probabilidad de una de las puertas y no de las dos por igual. Por eso el cálculo es incorrecto. (66%>33%)
Fijaros que la única manera de tener un 50% de probabilidades de ganar, es elegir cambiar de puerta o no al azar, ya que en este caso aunque una puerta sea mas probable, tenemos las mismas opciones de elegirla que la otra, por lo que las veces que cambiemos de puerta, compensará las veces que no lo hagamos. De todas maneras esto sigue siendo menos que cambiar siempre de puerta, aunque más que quedarnos siempre la puerta. (66%>50%>33%)
¿Curioso verdad?
Ahora sabemos que Monty Hall era un tipo muy astuto, al utilizar la psicología y las matemáticas. Si el concursante no cambiaba de puerta, tenía las de perder, y para tener ventaja tenía que arriesgarse y aceptar el cambio.
La realidad es que la mayoría de concursantes perdían el coche, porque muy poca gente se arriesgaba a cambiar la puerta. Quien cambiaría una puerta cuando pueden engañarte con la pregunta?. Tan solo un loco, o un matemático, y es que el engaño es precisamente eso.
¿Quién dice que las matemáticas no sirven para nada?
Si te interesan las matemáticas del juego puedes visitar mi canal de youtube math for all en Youtube donde estudio matemáticamente juegos de azar como Póker o Blackjack.