Las Matemáticas del Blackjack
AVISO: Este artículo no pretende fomentar el juego, ni la ludopatía. Se trata de un análisis enfocado en las matemáticas del juego, donde se explica si el juego puede ser rentable o no y como analizarlo.
¿Crees que se puede ganar en el Blackjack?. ¿Cual es la mejor manera de jugar? En este articulo resolvemos estas y otras cuestiones con la ayuda de las matemáticas.
1.Reglas del Blackjack
2.Acciones de Blackjack
3.Premios de Blackjack
4.Estudio matemático del Blackjack
4.1.Probabilidades de pasarnos de 21
4.2.Probabilidades de que el Crupier se pase de 21
4.3.Ventaja Matemática de la Banca
5.Estrategia Básica
5.1.Tabla Estrategia Básica 1 Mazo
5.2.Tabla Estrategia Básica Varios Mazos
6.Conteo de Cartas
7.Conclusiones
1.Reglas del Blackjack
El Blackjack es un juego de baraja francesa de hasta 7 jugadores donde los jugadores se enfrentan a la banca.
El objetivo es sumar 21 con nuestras cartas o un valor superior al de la banca sin pasarnos del número.
Si superamos 21 o sumamos un valor mas bajo que el del crupier automáticamente perderemos nuestra apuesta.
Una vez realizadas las apuestas se reparten 2 cartas visibles a cada jugador y solamente una para la banca.
Los jugadores deberán decidir en base a sus cartas y a la del crupier si quieren pedir carta, plantarse, doblar su apuesta o dividir su mano en manos separadas.
Todas las cartas valen el valor numérico que tienen del 2 al 10, excepto las figuras que valen 10, y el as que puede valer 1 o 11 a nuestro interés.
Los pagos se hacen a la par y podemos sumar 21 con más de dos cartas, pero solamente se considerará blackjack cuando se haga con dos, y estará por encima de cualquier 21 sumado con más cartas.
La banca solo puede pedir carta o plantarse, y solamente pide carta cuando su mano está por debajo de 17, por lo que si llega o supera ese valor se planta automáticamente.
En caso de que el crupier se pase de 21 los jugadores que todavía están en la mesa ganarán sus apuestas y en caso de empate el jugador recuperará su apuesta.
Se puede jugar a blackjack con una o más barajas, siendo 6 barajas en el Blackjack Europeo.
El Blackjack Americano tiene algunas diferencias en sus reglas que le permiten modificar si el crupier pide carta o de que maneras pueden dividir la mano los jugadores. Además este se reparte una segunda carta tapada después de repartir a los jugadores y puede consultarla en caso de que su primera carta destapada le de la posibilidad de hacer blackjack (si efectivamente suman 21 los jugadores pierden su apuesta antes ni siquiera de jugar). Esto hace que se agilice el juego y también disminuye la ventaja de la casa.
2.Acciones de Blackjack
-Pedir Carta/Plantarse
En primer lugar podemos pedir carta mientras nuestra suma no supere 21. Dependiendo de las cartas nos convendrá pedir otra carta o plantarnos pero si superamos 21 con la carta pedida perderemos la apuesta.
-Doblar Apuesta
Para doblar nuestra apuesta necesitamos una mano que sume obligatoriamente 9, 10 u 11 y solo podrá hacerlo en el principio de turno. En caso de doblar tu apuesta solo podrás recibir una carta más.
A diferencia en el Blackjack Americano podremos doblar con cualquier mano.
-Separar Cartas
Si nuestras cartas tienen el mismo valor, podemos separar en dos manos diferentes cada carta para jugarlas de manera independiente. Para eso es obligatorio añadir además una apuesta igual a la inicial. Tenéis que saber que dentro de una mano separada aunque sumemos 21 con la siguiente carta no se considerará blackjack.
Después de separar, la mayoría de casinos permiten doblar a las nuevas manos resultantes y esto nos da cierta ventaja. (No permitirlo aumenta la ventaja de la casa en un 0,12%.)
-Apuesta de Seguro
Si la carta descubierta por el crupier es un as, podemos apostar a seguro si presentimos que la banca conseguirá blackjack con la siguiente carta. Si finalmente lo consigue seremos premiados.
-Rendirse
Rendirse solo es posible en el Blackjak americano y si el jugador se rinde perderá la mitad de la apuesta.
3.Premios de Blackjack
–1 a 1 (una ficha por cada ficha apostada) si ganamos a la banca.
–3 a 2 (tres fichas por cada dos fichas apostadas o 1 ficha y media por cada ficha apostada) si ganamos a la banca con Blackjack (siempre que no se produzca un empate). En el Blackjack Americano de las Vegas se paga con 6 a 5.
–2 a 1 (dos fichas por cada ficha apostada) si ganamos una apuesta a seguro.
El caso del Blackjack Americano, también es habitual que si el jugador tiene blackjack y el crupier tiene un As visible, se le ofrezca la posibilidad de cobrar el blackjack con un 2 a 1 (en lugar del 3 a 2 habitual) como alternativa a la apuesta de seguro.
4.Estudio matemático del Blackjack
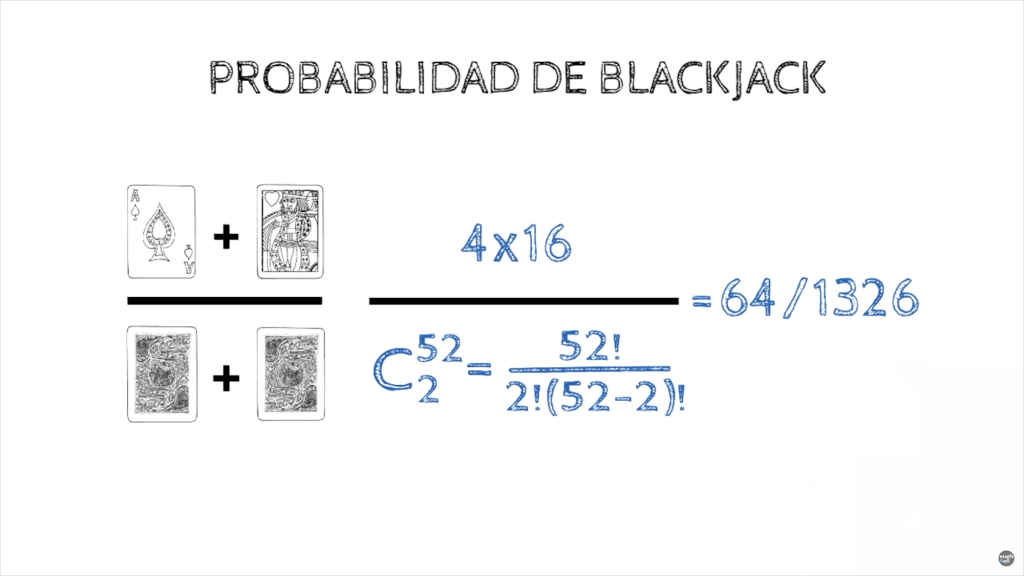
Para analizar el blackjack a nivel matemático debemos saber que una baraja francesa tiene 52 cartas.
-4 de ellas son As.
-16 de ellas son 10 o Figura.
-Las 32 restantes son números del 2 al 9.
Por lo que podemos sacar algunas conclusiones:
-Aproximadamente una tercera parte de las cartas tienen el valor 10 (Lo cual toma un papel fundamental).
-Solo hay 4 cartas que son as, por lo que si queremos obtener un blackjack vamos a necesitar uno de ellos, pero cual es la probabilidad?
La probabilidad de obtener blackjack sería las maneras que tenemos de obtener 21 con dos cartas de entre todas las combinaciones posibles de sacar 2 cartas de la baraja.
O lo que es lo mismo casos favorables entre casos posibles.
para obtener 21 con dos cartas necesitamos un as y un 10 , y en la baraja existen 4 ases y 16 10’s (entre figuras y cartas de valor 10).
Por otra parte todas las combinaciones de sacar 2 cartas, son combinaciones de 52 elementos cogidos de 2 en 2 (donde no importa el orden y no se pueden repetir),
por lo que la probabilidad es:
4.16 / C52,2 que es igual a 64/1326 o lo que es lo mismo un 4,8% de probabilidad (lo cual era lógico ya que sabemos que para tener blackjack necesitamos siempre un as y tan solo hay 4 en la baraja)
-En caso de jugar con varias barajas se mantiene la misma proporción de cada figura o número, ya que es lo mismo 4 ases en 52 cartas que 8 en 104. Pero las probabilidades de obtener un resultado concreto varían ligeramente, ya que influye menos quitar una carta a una baraja de 104 cartas que a una 52. Por lo que cada juego con diferentes barajas tiene su propio estudio probabilístico.
4.1.Probabilidades de pasarnos de 21
Para calcular la probabilidad de pasarnos de 21, debemos calcular la probabilidad de pasarnos para cualquier mano, y para eso necesitamos ir mano por mano.
Imaginémos que nuestra mano por ejemplo suma 12:
Al pedir una carta más estos se nos plantean todos estos casos:
Como vemos a priori hay 4 casos de 13 donde superamos 21. Esto es aproximadamente una probabilidad del 30%, lo que significa que con un 12 solo en un 30% de las veces que pidamos carta nos pasaremos de 21.
El cálculo de esta probabilidad es una simplificación porque realmente tendríamos que tener en cuenta que las cartas que conforman el 12 varían ligeramente la probabilidad de la carta hemos pedido, pero la diferencia con este cálculo no es muy grande y además es mucho más complejo de estudiar y de entender)
Si calculamos lo mismo para todas las manos posibles (y de manera exacta) obtenemos la siguiente tabla:
Como véis a partir de 13 tanto nosotros como la banca nos pasaremos la mayoría de veces.
Fijaros también que si nuestra suma es 11 o menos nunca podremos superar 21 con una carta más por eso su probabilidad es 0
4.2.Probabilidades de que el Crupier se pase de 21
Como acabamos de ver, si no queremos perder la mayoría de veces debemos pedir carta, siempre y cuando nuestra mano sume menos de 14. La pregunta es, ¿poniéndonos un límite en 14 tenemos opciones de ganar?
Si tenemos en cuenta que la banca siempre pide carta hasta sumar 17 o más, plantarse con un valor menor a 17 solo te hace ganador cuando el crupier se pasa.
O dicho de otra manera, si el crupier no se pasa de 21, su mano siempre tendrá un valor igual o mayor a 17, por lo que los jugadores que se plantaron con una mano menor a 17 perderán su apuesta.
Pues bien según el estudio matemático realizado las probabilidades de que el crupier se pase en función de la carta que tiene (y a su estrategia) son las siguientes:
Para una carta alta la probabilidad de pasarse es bastante baja siendo el as la carta que mas ventajas le ofrece a la banca.
Para una carta baja la probabilidad es mas alta, pero fijaros que en ningún caso supera el 50%.
Si hacemos el promedio de todas llegamos a la conclusión de que el crupier se pasa en un 28.35% de las veces (368,67/13) lo que significa que en el 71.65% de las veces que te plantes con menos de 17 vas a perder tu apuesta.
Límite de la Banca
Como acabamos de ver es inútil ponerse un límite por debajo del de la banca, ya que perderemos en la mayoría de ocasiones.
Pero gracias a esto también hemos visto que la primera carta del crupier nos puede dar una información valiosa para tomar decisiones.
Las preguntas que nos surgen entonces son:
-¿Por qué el límite de la banca es 17?
-¿Qué pasa si copiamos esta estrategia y nos plantamos a partir de 17?
4.3.Ventaja Matemática de la Banca
Si os fijáis el crupier siempre espera que el jugador termine su jugada antes de proceder a jugar él. Esto significa que si el jugador se pasa de 21, pierde su apuesta, independientemente de lo que haga el crupier. Por lo que si el crupier también se pasa de 21 sigue siendo el jugador el que pierde, ya que se había eliminado antes. Eso hace que la banca gane en un escenario que a priori es de empate, y esto ocurre el 7,9% de las veces que se juega. Eso es aproximadamente un 8% de ventaja sobre el jugador que finalmente se reduce a un 5,6% si tenemos en cuenta que los blackjacks se pagan 3 a 2 en vez de los 2 a 1 equitativos. Esa es la principal ventaja del casino.
Para luchar contra esto, el jugador tiene opciones que le permiten tener una estrategia flexible. Puede doblar cuando le interesa, abrir manos o rendirse, y lo más importante, conoce una carta del crupier que le hará tomar decisiones distintas de pedir o plantarse teniendo en cuenta ésta. Y aquí es donde entran las matemáticas una vez más:
5.Estrategia Básica
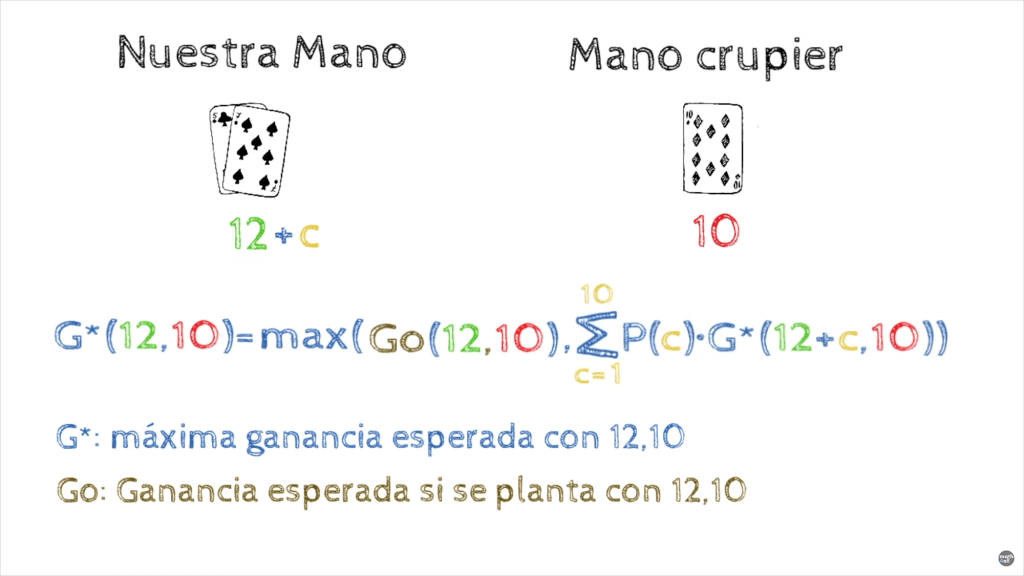
En los años 50 un grupo de matemáticos líderados por Roger Baldwin desarrollaron la estrategia básica. Esta se basa en optimizar las decisiones del jugador de tal manera que la acción que elija es la mas óptima en cuanto a ganancia de entre todas las acciones que puede tomar. Esto nos brinda a priori la máxima ganancia posible a largo plazo.
Y se consigue elaborando un modelo probabilístico que calcula en base a la mano del jugador condicionada por la carta del crupier cuando es mas óptimo tomar la decisión de plantarnos, pedir carta doblar, separar, o apostar a seguro, ya sea para para manos duras que son inflexibles como para manos blandas donde hay un as y puede cambiar la suma.
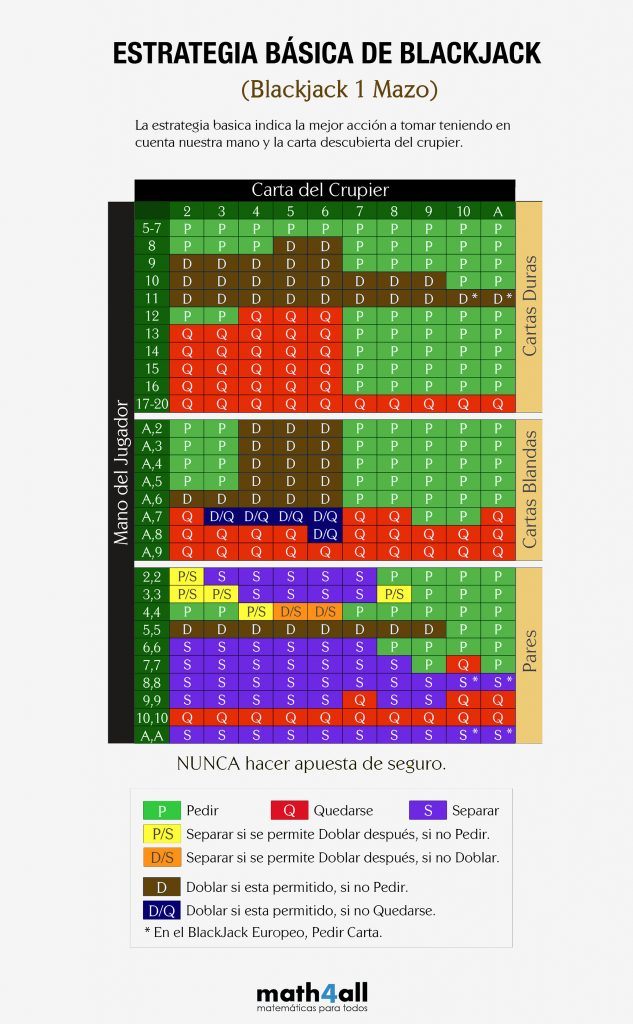
En el lenguaje matemático podemos decir que mediante una función recursiva con unos valores finales definidos, y una tabla con todas las probabilidades para la suma del crupier, se calcula el máximo entre la ganancia esperada si se planta y la ganancia esperada teniendo en cuenta todas las posibles cartas que pueda recibir al pedir carta (el promedio de todas las posibles ganancias esperadas si pide la siguiente carta). Con esto se elabora una tabla de resultados que nos aseguran matemáticamente cual es la acción mas conveniente, haciendo que nuestra estrategia sea óptima sea cual sea la combinación de cartas entre el jugador y el crupier. Por lo que si queréis jugar bien al Blackjack os recomiendo que os descarguéis esta tabla:
DESCARGAR ESTRATEGIA BÁSICA 1 MAZO
DESCARGAR ESTRATEGIA BÁSICA VARIOS MAZOS
Como detalle fijaros que en las manos duras a partir de 17 nos da instrucciones de plantarnos, lo que significa que independientemente de la carta que tenga el crupier las matemáticas nos dicen que la ganancia esperada es siempre más alta si nos plantamos. Eso responde a la pregunta de porque la casa pone 17 como límite, si entendemos que la banca también es un jugador.
Fijaros también que nunca debéis apostar a seguro. Esto es debido a que aunque la banca tenga un AS en su mayoría de veces no conseguirá Blackjack.
Pues bien, con esta estrategia pasamos del 5,6% anterior a un porcentaje inferior al 1% para la banca que oscilará dependiendo de las reglas de la mesa y de las barajas que se utilicen. Tenemos que entender que aunque se trate de una estrategia óptima no implica que necesariamente sea una estrategia ganadora, pues el balance de nuestra ventaja pese a ser pequeño sigue siendo negativo. Y esto se debe principalmente a que las cartas altas del crupier disminuyen en mayor medida nuestra ventaja que las cartas bajas, por lo que aunque tomemos la mejor decisión, no ganaremos necesariamente, aunque si jugaremos de la mejor manera posible.
En el Blackjack americano los porcentajes son ligeramente diferentes pero en ningún caso superan el 1%, siempre y cuando apliquéis una estrategia básica adaptada para estas reglas, recordad que cada modalidad es diferente y necesita una estrategia básica diferente.
Análisis Estrategia Básica
Si la manera mas óptima de jugar tan solo minimiza las pérdidas, ¿existe una manera real de ganar en el blackjack?
Para responder a esta pregunta debemos entender que hipótesis se han hecho para resolver este problema.
La estrategia básica se desarrolló teniendo en cuenta que las probabilidades de cualquier cada carta son invariables a lo largo del juego, es decir la probabilidad que aparezca un as, un número o una figura son siempre las mismas. cosa que no es del todo real ya que las probabilidades van cambiando a medida que se van repartiendo las cartas.
Pero que pasaría si os dijera que podemos tener un sistema para contar estas cartas, y anticiparnos a más manos ganadoras?
6.Conteo de Cartas (Sistema HI-LO)
A este sistema de conteo se le conoce como HI-Lo y lo escribió por primera vez en 1962 un matemático ex empleado de IBM en el libro “Beat the dealer”
La idea es controlar las cartas altas de la baraja, que son las únicas que pueden conformar blackjack, de tal manera que si sabemos cuantas cartas altas han aparecido sabemos si quedan muchas o pocas por aparecer, y así podemos saber que probabilidades tenemos de obtener blackjack en tiempo real, con la ventaja adicional que eso supone.
Para conocer esa ventaja necesitamos tener un control sobre las cartas que van apareciendo, algo que parece ser bastante complicado si para esto necesitamos memorizar todas las cartas que van apareciendo. Afortunadamente las matemáticas nos ofrecen una solución mejor.
El sistema Hi-Lo asocia a las cartas a tres valores diferentes -1, 0 y 1.
1 negativo a las cartas altas, 1 positivo a las cartas bajas y las restantes adquieren un valor nulo o 0.
Nuestro cometido es entonces llevar la cuenta de todas las cartas que se han repartido incluida la del crupier.
Dado que en este sistema existe la misma proporción de cartas altas y bajas, una cuenta positiva o negativa nos indica directamente cuando quedan o no más cartas altas en la baraja.
Por lo que si nuestra cuenta es negativa es porque habremos contado más cartas altas, y quedarán menos cartas altas por aparecer, algo que no nos interesa.
En cambio si nuestra cuenta es positiva es porque habremos contado más cartas bajas, y sabremos con certeza que quedan más cartas altas por aparecer. Es aquí donde podemos sacar provecho.
Nuestro objetivo con este sistema es acumular en esa cuenta un número positivo lo mas grande posible que nos ofrece las mayores probabilidades de obtener blackjack. Si lo conseguimos podemos decir que la mesa está caliente y podemos modificar la estrategia básica a nuestro interés por ejemplo para doblar la apuesta o apostar a seguro. Como el blackjack se paga 3 a 2 y los casos de empate son poco probables tenemos por primera vez un sistema de juego con una ganancia esperada superior a la de la banca. Y todo gracias a las matemáticas.
Fijaros que las cartas bajas equilibran a las altas, lo que implica que la cuenta total una vez se hayan repartido todas las cartas tiene que ser 0 obligatoriamente. Además también vemos que hay 3 cartas que no se consideran ni altas ni bajas, esto se debe a que el sistema tiene que equilibrar 5 altas con 5 bajas, pero en la baraja hay mas números que figuras ases y dieces por lo que hay 3 números sobrantes que se agrupan en un valor neutro que no interfiere sobre la suma.
En el caso de jugar con varias barajas hay que tener en cuenta que no es lo mismo una suma con 4 barajas pendientes que la misma suma con 1. Por eso tenéis que ir dividir la suma actual entre el número de barajas que creemos que quedan por salir, y esta será la cuenta real.
Existen otros métodos de conteo algo más eficientes pero asignan mas valores y son algo más complicados de ejecutar, pero si entendéis el HI-LO entenderéis cualquier otro.
Pese a que podemos tener una ventaja con este sistema todo esto sucede tras miles y miles de manos y nos da una ventaja de décimas de porcentaje, por lo que váis a necesitar una cartera muy grande y mucho tiempo.
Medidas actuales contra el Conteo de Cartas
Lamentablemente los casinos han introducido medidas para contrarrestar a los contadores de cartas.
-La primera es aumentar el número de barajas, y es que que a más barajas use el juego más complicado lo váis a tener para ganar contando. Pensad que el echo de que existan mas barajas pendientes hace que sea mas difícil acumular solamente las mejores cartas al final que con una sola baraja, eso hace que la varianza de la cuenta que estáis llevando sea mas pequeña y en consecuencia tengáis menos posibilidades.
Una: 0,17%
Dos: 0,46%
Cuatro: 0,60%
Seis: 0,64%
Ocho: 0,66%
-La segunda medida que se aplica actualmente son los mezcladores y elementos automáticos para mezclar las cartas antes de que termine el juego, que obligan al contador a reiniciar la cuenta que llevaba acumulada y por lo tanto perder toda la ventaja.
-Además algunos casinos como en Las Vegas pagan 6 a 5 por el blackjack lo cual triplica la ventaja de la casa sobre el jugador e incluso en algunos si sospechan que un jugador es contador se pueden permitir el lujo de modificar la apuesta de la casa.
Tenéis que saber que el conteo es legal pero si os descubren os expulsarán del casino. Los casinos conocen el perfil de un contador de tal modo que no les será muy complicado descubriros si empezáis a ganar dinero.
7.Conclusiones finales
Desde el punto de vista de los números si existe una posibilidad matemática de ganar al blackjack por eso mucha gente ha ganado dinero, pero no es sencillo de ejecutar, ni rápido, ni mucho menos barato por lo que probablemente no esté a tu alcance.
En cualquier caso si váis a jugar:
- Os recomiendo aprender y adaptar primero la estrategia básica para mejorar tus probabilidades.
- No apostar en mesas con premios inferiores a 3 a 2.
- Jugar en mesas con el número de barajas más pequeño posible y revisar muy bien las reglas de la mesa.
- Y si vas a contar cartas, estudiar como se mezclan y probar primero tu estrategia antes de invertir una gran cantidad.
Recordad que:
- A mas barajas, más gana la casa.
- A peores reglas, más gana la casa.
- Y a menos estrategia o conocimiento tienes, más rápido y seguro gana la casa.
Entonces la casa siempre gana?
No siempre gana, pero está claro es que si no lo hace cambiará lo que sea necesario para hacerlo. Recordad que esto es un negocio.









Buenas,
Te felicito por tus explicaciones.
Son muy profesionales y con sentido común, realmente enseñas muy bien.
Llevo tiempo jugando Martingala en la ruleta con excelentes resultados.
En los últimos 15 años he tenido buenas ganancias, aunque ya no voy tan seguido pues es igual que ir a trabajar. y prefiero mi trabajo.
Lo que diferencia mi juego de la Martingala tradicional es que espero a que se repita 5 veces un color para jugarle al contrario. Juego solo 4 veces y si pierdo lo doy por perdido.
Realmente son pocas las veces que se dan más de 9 colores seguidos y si pasa son muchísimas más las que no.
Por eso el resultado me ha sido positivo.
Ahora bien, mi consulta para ti.
Si estáis jugando al Black Jack con la tabla básica… ej. de a U$S 25 y luego de 2 o 3 veces seguidas que la banca te gana, comienzas a apostar U$S 100, 200, 400 y hasta 800. (Martinagala en el back jack luego de perder 3 veces con una suma 4 veces tu apuesta inicial)
Si ganas vuelves a tus 25 cada mano.
De ésta forma, no tendrías más chances de ganar que la banca casi siempre?
Espero tu respuesta cuando tengas el tiempo y te pido mantenerlo en reserva por al menos unos meses si es que funciona.
Hagamos algo de dinero y luego si lo subes a Youtube, vale?
Te dejo un gran saludo y estamos en contacto.
Amigo cual fue tu apuesta inicial con la que empezaste este martingala que manifiestas y cual fue la máxima apuesta inicial que realizaste que aún te dio beneficios. Gracias por la respuesta.
hola diego
puse en practica tu metodo que explicaste en black jack y por dos dias seguidos me dio un resultado positivo pero aun asi me gustaria saber si tu lo has utilizado
y si cuando pierdes 2 manos seguidas a la tercera la ganas vuelves a empezar de cero o solo rebajas una perdida y sigues bajando a llegar de cero de nuevo? yo hice esto y tuve una ganancia de 5 mil dolares cada dia como meta solo metiendo 1,500.
saludos
Diego, tu metodo de Martingala no tiene una logica matematica y esta basado solamente en supersticion, las probabilidades de que salga un color son las misma SIEMPRE, independientemente de que ya alla salido 100 veces el mismo color, las posibilidades siempre van a ser las mismas, es como cuando haces un volado con una moneda, tienes 50% de probabilidad de cara y 50% de cruz, el hecho de que salieran 10 caras seguidas no aumenta la posibilidad de que en el siguiente tira salga cruz, ten eso en cuenta al jugar, realmente eso de esperar a que salgan 3 colores seguido no funciona, por ue la probabilidad no cambia
Eso no es del todo cierto, o sea a posteriori, una vez que ya ha salido una racha de por ejemplo 100 caras como tú dices, la probabilidad de que la siguiente sea cara es del 50% y hasta ahí todos de acuerdo.
Sin embargo si la situación es antes de eso, la probabilidad de que salieran 101 caras seguidas es prácticamente 0, ya que a no ser que esté trucada la moneda, debe salir cruz alguna vez en 101 rondas seguidas.
De hecho, la racha más larga en una ruleta europea es de 26 veces seguidas el mismo color.
Si la martingala no funciona, es porque hay un límite máximo de apuesta
Como si juegas a partir del 8º color! Tienes exactamente la misma probabilidad de perder que si lo haces con el 1º o el 2º o el 3º,… es una hiperbola. (tiende a 0).
si tienes un 1% de ganar 99€ tienes 99% de perder 1€, sin contar el “0” y “00”.
Si la ruleta no tuviera ceros, con la ruleta siempre regresarías a la cantidad inicial jugada.
La ruleta es perfecta, solo habia 3 jugadas capaces de cambiar la “ventaja” y ya se modifico el precio de las jugadas para anular estas.
Si me he equivocado en algun calculo, porfavor enviarme un correo.
Hay algo que no entiendo de la estrategia basica, si tengo 12 yo vs 10 de la banca, y pido carta, me viene un 4 por ejemplo, tengo 16, ahi vuelvo a pedir? o planto?
Porque la probabilidad de que la banca llegue a 17, sigue estando en el 70 / 75%…, o si pido y me dan un As, tengo 13, pido otra y viene un 2, tengo 15? En ningun sitio dice hasta cuantas cartas pedir…
Yo Me quede con la misma duda, yo pienso ya más bien es de sentido común y estrategia, si tienes 15 tienes del 1-6 de acertar carta y del 7-13 de pasarte, más del 50% así que ya viendo los números en cada caso ya tu decides
Buenas Rodrigo, usar el sentido común es bueno, pero tienes que tener en cuenta que la carta que tiene el crupier también puede cambiar tus decisiones. Es decir no solamente es calcular con tus valores lo que te irá mejor, porque aunque eso sea así, es posible que si el crupier tiene ciertas cartas, necesites evaluar tu decisión en base a las probabilidades que tiene el crupier, que dependen como te he dicho de su carta. Por eso existen esas tablas, porque son mejores que si aplicas solamente la probabilidad simple. Saludos!
Buenas, con un 16 contra un 10 de la banca, y jugando la banca con varios mazos, debes rendirte si puedes, y sinó pedir carta, pero nunca plantarte. Ten en cuenta que la probabilidad de que el crupier se pase está calculada para antes de empezar el juego, pero una vez tiene un 10 y tu un 16 sus probabilidades y las tuyas cambian. Ese cálculo es general, pero en cada caso es diferente, por eso un 16 contra un 10 de la banca hay que calcularlo realment, y es complicado saber exactamente cuales son, porque no son cálculos fáciles, por eso se han hecho esas tablas.
Saludos!
Y aparte de eso esa jugada en específico es perdedora 16 vs 10 si te quedas en el largo plazo perderas dinero y si pides en el largo plazo seguiras perdiendo PERO PERDERAS MENOS V😉🤫
Hola buenas:
Acabo de empezar con el conteo de cartas y estoy teniendo algunos problemas a la hora de manejar el dinero.
Los contadores de cartas profesionales saben cual es su riesgo de ruina mediante algunas aplicaciones de pago, pero como yo ando justo de dinero, prefiero invertir cada centavo en el juego.
Se de una pagina que te dice el riesgo de ruina, pero para ello tienes que saber la desviación estándar por 100 manos. He intentado sacarla mediante una ecuación que aprendí en clase, pero como mis conocimientos matemáticos son limitados no he conseguido nada.
¿Me podrias decir como se saca la desviación estándar por cien manos? Es muy importante para mi.
Gracias
Paso 1: calcular la media de las 100 manos (esto es sumar todos los datos y dividirlos entre 100)
Paso 2: Restar a cada dato la media y elevar esa resta al cuadrado (en el paso 3 utilizarás estos resultados)
Paso 3: sumar los valores que resultaron del paso 2.
Paso 4: dividir el resultado del paso 3 entre 100.
Paso 5: sacar la raíz cuadrada.
Comentario: Decir “más óptimo” es redundante. Es lo equivalente a decir “subir para arriba” o “bajar para abajo”. Cuando algo es óptimo es porque es eso: óptimo. Ya no se puede mejorar. Por lo tanto con que digas “óptimo” es más que suficiente, no se requiere el “más”.
Fuera de eso, me gustó el artículo.
Te agradezco la explicación, soy consciente de que no es correcto decirlo así, pero el lenguaje natural a veces juega malas pasadas. Me alegro de que a parte de eso te gustase el artículo. Aunque me hubiera gustado también algún detalle en lo positivo, ¡un saludo!
Hola. Hay un estimado de cuantas manos seria lo optimo en dejar jugar a la banca mientras no se pase para luego comenzar a jugar con martingala incrementando la probabilidad asi de ganar ??
No te recomiendo hacer eso. Piensa que lo que haga el crupier en cada partida es independiente de lo que sucedió antes. En matemáticas se le llama un “suceso independiente” y también ocurre por ejemplo en la ruleta. Mucha gente piensa que porque salga muchas veces el rojo, hay más probabilidades de que salga el negro en la siguiente tirada, pero no es así, porque el resultado depende solo de un tiro que no tiene recuerdo de lo anterior porque es físico. Lo mismo pasa en el Blackjack, una vez se baraja, aunque el crupier lleve mucho tiempo sin pasarse, la siguiente vez sigue teniendo la misma probabilidad de pasarse. Por eso empezar antes o después de la martingala no te dará ninguna ventaja. Te recomiendo leer la sección de preguntas mas frecuentes del articulo de la ruleta que tienes en la misma web, donde justamente hablo sobre la martingala. Saludos!
Muy buenas tus explicaciones
Muchas gracias, no olvides suscribirte al canal de Youtube!
Hola. Es muy bueno el articulo. Felicitaciones. Ya hice una consulta pero hago esta. Si la probabilidad de sacar BJ tanto para la banca como para el player es de 4.8 % por 4 ases por baraja, la duda que me surge es esta, sobre todo si la banca muestra un As. Cuando aparece el As, cual es la probabilidad que saque BJ. Esto lo pregunto porque se recomienda en el articulo no apostar a seguro por la poca probabilidad que salga BJ pero sobre la base que la misma es de 4.8 % pero entiendo que si la banca muestra un AS y es ahi cuando pide seguro, la probabilidad es mayor por cuanto hay muchas mas figuras y 10 a aparecer. Muchas gracias por tu articulo y analisis.
Muchas gracias, es correcto lo que dices, las probabilidades cambiarían al tener el Croupier un As. Y efectivamente son mayores a un 4.8%, pero normalmente siguen siendo una probabilidad inferior al 50%. Piensa que en la baraja solo hay 16 cartas que le servirían para hacer Blackjack, de las 42 que tiene la baraja menos las que se han destapado que serían 2 tuyas y la suya. Eso es una probabilidad de 16/39=0,4->40%. Pero es verdad que hay algún caso donde podrían superar el 50%, por ejemplo si jugasen 7 jugadores (que es el máximo permitido) y ninguno de ellos tuviera ninguna figura o 10, serían 16/(42-(7*2))=0,57->57% y en ese caso si te interesaría apostar a seguro, pero en general es una situación muy complicada, ya es muy difícil que de 7 jugadores ninguno tenga figura. Por eso te dicen que normalmente no apuestes a seguro. Además hay otra situación interesante donde podrías apostar a seguro que es cuando tu tienes Black-Jack y el croupier tiene un as, ya que el beneficio promedio de esos enfrentamientos te sale mayor en teoría si apuestas a seguro que si no lo haces. Pero al ser tan difícil repetir esa situación varias veces en una misma partida, si no juegas durante mucho tiempo, perderás normalmente, por lo que tampoco te lo recomiendo. Saludos!
¿Cuál es su nombre? Disculpe si lo incomode, lo que sucede es que quiero citar la información y no sé su autoría. Espero su respuesta pronto. Muchísimas gracias de antemano.
Autoría soy yo, el artículo es mio, puedes poner math4all.